Minimum Spanning Tree와 Prim 알고리즘에 대해 설명하기 전, 먼저 Spanning Tree의 정의부터 살펴보자.
Spanning Tree란 그래프 중 모든 정점이 간선으로 연결되어 있고 간선 간의 싸이클이 없는 그래프를 의미한다.
여기 앞에 Minimum이 붙으면 각 간선간의 weight의 총합이 최소가 되게 연결이 되는 그래프를 뜻하는 것이다.
즉, 모든 vertex가 다 연결되도록 spanning tree를 만드는 방식이 여러 개가 있을 때 그 중 간선의 합들이 최소가 되도록 연결하는 것을 의미한다.
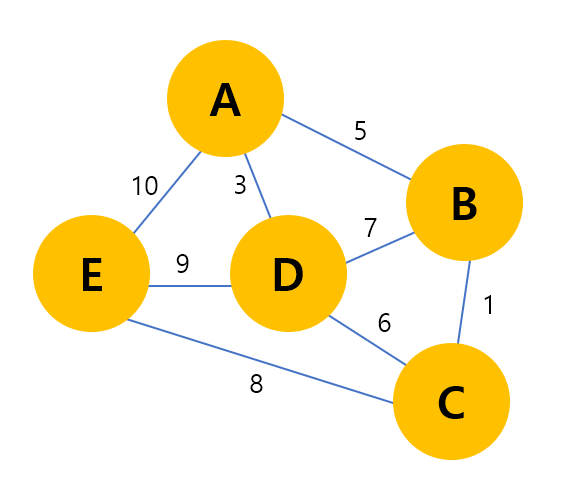
즉 위와 같은 그래프에서는 Minimum Spanning Tree는 아래와 같은 모양이다.
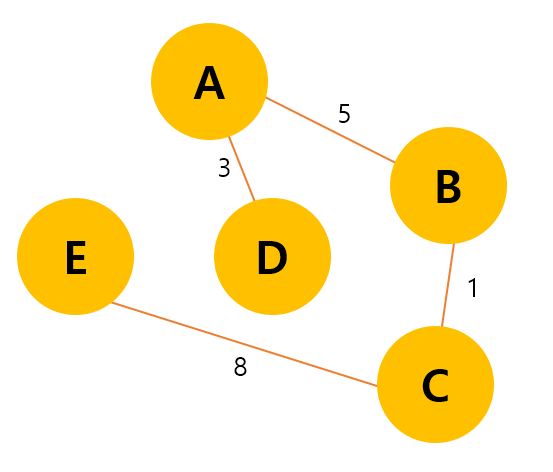
연결하는 다른 방법도 있지만 위와 같이 연결하면 총 weight가 최소가 된다.
그렇다면 위와 같이 Minimum Spanning Tree를 구하기 위한 알고리즘에는 무엇이 있을까. 대표적으로
1. Prim 알고리즘
2. Kruskal 알고리즘
이렇게 두 가지가 있다.
오늘은 이 두 가지 방법 중 Prim 알고리즘을 사용하여 Minimum Spanning Tree를 구하는 방식에 대해 알아보겠다.
Prim 알고리즘의 순서는 아래와 같다.
1. 모든 정점 (vertex) 중 아무 시작 정점을 고른다. (어짜피 모든 정점이 다 포함되어야 하기 때문에 시작 정점이 중요하지 않다)
2. 해당 정점에 연결된 정점 중 가장 최소의 비용을 가진 정점을 선택한다.
3. 이런 식으로 선택된 정점이 하나씩 늘어나는 것인데, 계속해서 선택된 정점들의 집합과 연결된 간선 중 가장 비용이 작은 간선을 선택한다. 이미 선택된 정점은 다시 선택될 수 없다.
4. 모든 정점이 선택될 때까지 이 과정을 계속 진행한다.
위와 같은 예시를 사용하여 Prim 알고리즘을 설명해보겠다.

먼저 1번에 따라 아무 정점이나 선택해본다. 나는 A 정점을 선택해보겠다. 그러면 다음으로 선택될 수 있는 정점에는 A와 연결된 B, D, E 정점이 가능하다. 각각 간선의 비용을 살펴보면 5, 3, 10이므로 그 중에서 가장 작은 3의 비용으로 연결된 D를 선택한다.
그러면 지금까지 아래와 같이 A와 D가 선택된 것이다.

그러면 다음 정점으로 가능한 것은 선택이 되지 않은 정점 중 A, D와 연결된 정점이다. 5와 7의 간선으로 연결된 B, 10으로 연결된 A, 6으로 연결된 C 모두 가능하다. 이 중 간선의 최소값은 5이므로 B가 다음 정점으로 선택되는 것이다.

그러면 이제 가능한 edge는 1의 간선, 6의 간선, 9의 간선, 10의 간선이다. 그 중에서 마찬가지로 1이 가장 작으므로 C가 선택된다.

다음으로 가능한 간선은 8, 9, 10이고 그 중에서 가장 작은 weight가 8이므로 8 간선이 선택되고 E가 채택된다.
E가 채택되면 모든 vertex가 선택되는 것이기 때문에 지금까지 선택된 edge를 다 연결하면

이렇게 연결이 되는 것이다.
프림 알고리즘은 음수인 간선에 대해서도 가능하며 이를 자바 코드로 구현하는 방법에 대해서는 다음 포스팅에서 살펴보도록 하겠다.
'알고리즘' 카테고리의 다른 글
| [BOJ 3584번] 가장 가까운 공통 조상 Tree 구조에서 찾아보기- Java (0) | 2021.08.31 |
|---|---|
| Prim 알고리즘 자바로 구현 (백준 1197번) (0) | 2021.08.30 |
| Dijkstra PriorityQueue 사용해서 구현해보기 ([백준] 1753번) (0) | 2021.08.29 |
| 위상정렬 Topological Sort 개념 + 시간복잡도 (0) | 2021.05.09 |
| [백준] 11058번: 크리보드 문제 다이나믹 프로그래밍으로 풀기 (0) | 2021.04.29 |






최근댓글